Kirchhoff's Circuit Laws

2023-12-06, RB

Wikipedia (en)

Kirchhoff's Circuit Laws consist of two rules:

1. Junction Rule (Current)
2. Loop Rule (Voltage)

• University Physics II - Thermodynamics Electricity and Magnetism (OpenStax)
  10.04 Kirchhoff's Rules

It is based on the conservation of charge.

$\sum_1^n I_k = 0 $

The sum of currents into a junction is equal to the sum of currents out of that junction.

Equivalent expression: The sum of all currents of a junction is zero, if you grade currents into the junction positive and those out of that junction negative.

It is based on the conservation of energy.

$\sum_1^n V_k = 0 $

The sum of the voltages around any closed loop in a circuit is equal to zero.

• Loops and currents (directions) are labeled arbitrarily.
  (You choose a direction and in the end you find out whether the assumption was right, e.g. whether current is flowing in that direction or in the opposite indicated by a negative current value.)

When summing voltages:

• Define a loop direction for all loops, e.g. clockwise.
• If you travel across a voltage source from low to high (from neg. to pos. terminal of that power supply) the voltage is positive; if you are traveling from high to low (from pos. to neg.) the voltage is negative.
• If you follow the current through a resistor the voltage is negative (voltage drop); if you oppose the current through a resistor the voltage is positive (voltage lift).

I did not find out yet, who the teacher behind NunezPhysics is! I could not ask for permission.

The following video tutorials discuss an example and describes very clearly how to derive the linear equation system from Kirchhoff's laws applied to an electrical circuit.

Fig.: Kirchhoff's laws examples from the NunezPhysics video tutorials above.

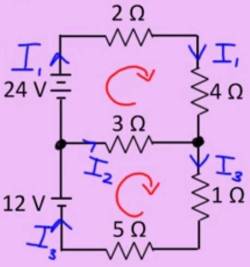
To solve the above problem we need three independent equations for three unknowns $I_1$, $I_2$, and $I_3$.

• (1) Left junction: $ -I_1 -I_2 + I_3 = 0$
• Right right junction: Redundant. No new information. Skip it. ( $ +I_1 +I_2 - I_3 = 0$ )
• (2) Upper loop: $ 24 - 2I_1 - 4I_1 + 3I_2 = 24 -6I_1 +3I_2 = 0 $
• (3) Lower loop: $ -3I_2 -1I_3 -5I_3 + 12 = -3I_2 -6I_3 + 12 = 0 $
• Outer loop: Sum of outer and inner loop. No new information. Skip it.

The resulting equation system of three equations in matrix form (i-th equation in i-th row):

$\begin{pmatrix} -1 & -1 & 1 \\ -6 & 3 & 0 \\ 0 & -3& -6 \end{pmatrix}\begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} 0 \\ -24 \\ -12 \end{pmatrix} $

To solve the above problem we need three independent equations for three unknowns $I_1$, $I_2$, and $I_3$.

• (1) Left junction:
  $ -I_1 -I_2 + I_3 = 0A$ → multiply by $1\Omega$
  $(-1\Omega) I_1 + (-1\Omega)I_2 + (1\Omega)I_3 = 0A\Omega = 0V$

• Right right junction: Redundant. No new information. Skip it.
  ( $ +I_1 +I_2 - I_3 = 0A$ )

• (2) Upper loop:
  $ 24V + -2\Omega I_1 + -4\Omega I_1 + \Omega 3I_2 = 24V + (-6\Omega)I_1 + (3\Omega)I_2 = 0V $

• (3) Lower loop:
  $ -3\Omega I_2 -1\Omega I_3 -5\Omega I_3 + 12V = (-3\Omega)I_2 + (-6\Omega)I_3 + 12V = 0V $

• Outer loop: Sum of outer and inner loop. No new information. Skip it.

The resulting equation system of three equations in matrix form (i-th equation in i-th row):

$\begin{pmatrix} -1 & -1 & 1 \\ -6 & 3 & 0 \\ 0 & -3& -6 \end{pmatrix}\Omega\begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix}A = \begin{pmatrix} 0 \\ -24 \\ -12 \end{pmatrix}V $

Devide by $\Omega A$ (=$V$)$:

$\begin{pmatrix} -1 & -1 & 1 \\ -6 & 3 & 0 \\ 0 & -3& -6 \end{pmatrix}\begin{pmatrix} I_1 \\ I_2 \\ I_3 \end{pmatrix} = \begin{pmatrix} 0 \\ -24 \\ -12 \end{pmatrix} $

This code block shows the solution of the LES in Matlab/Octave. Klick on the block title to download.

kirchhoff_exercise_01.m

# kirchhoff_exercise_01.m
# This script solves a simple LES resulting from Kirchhoff's laws.
# Example from NunezPhysics video tutorial: https://www.youtube.com/watch?v=zdE7xsbuNTg
# R. Becker, 2015-04-12 
 
# A*x = b <=> x = A^-1 * b (another notation x = A\b)
 
A = [-1 -1 1 ; -6 3 0 ; 0 -3 -6]
 
b = [0 -24 -12]' # ' means "transpose". Here result is column vector
 
x = A\b
 
# alternative: 
# x = A^-1 * b
# or 
# x = inv(A) * b

This code block shows the solution of the LES in Python (numpy). Klick on the block title to download.

kirchhoff_exercise_01.py

# kirchhoff_exercise_01.py
# This script solves a simple LES resulting from Kirchhoff's laws.
# Example from NunezPhysics video tutorial: https://www.youtube.com/watch?v=zdE7xsbuNTg
# R. Becker, 2021-10-23 
 
import numpy as np
 
# A matrix is an array of rows, which are arrays. Thus a matrix is a two dimensional array.
# The numpy.array() function is used to create 2D array (aka matrix) from a list of row lists.
R = np.array(
    [
        [-1.0, -1.0,  1.0],
        [-6.0,  3.0,  0.0],
        [ 0.0, -3.0, -6.0]
    ])
 
V = np.array([0.0, -24.0, -12.0])
 
# Inverse matrix
Rinv = np.linalg.inv(R)
 
# Matrix vector multiplication, aka dot product
I = Rinv.dot(V)
 
# Print currents
print(I)

• How to Solve a Kirchhoff's Rules Problem - Simple Example, by Jesse Mason