This is an old revision of the document!
Table of Contents
Solar Dish with Stirling Engine
Topics
Stirling cycle, concentrated solar power, solar irradiance, global radiation
Introduction
Concentrated Solar Power
The principle of concentrated solar power (CSP) is used in solar thermal power plants. Incoming irradiance is concentrated by mirrors and focused on a thermal collector, where a medium is heated. The most common approach is to use parabolic troughs heating up collector pipes in the focal line of the troughs. The collector pipes are filled with a heat transfer fluid transporting the thermal energy to a heat engine (e.g. a steam turbine) connected to an electrical generator.
Another way - for several reasons less common - is the use of a parabolic mirror (aka “dish”) focusing on the hot end of a Stirling engine.

Fig.:Solar dish-Stirling generator consisting of a parabolic mirror and a Stirling engine.
Source: https://de.wikipedia.org/wiki/Solar-Stirling (de. Use Google translate for en)
Irradiance Maps
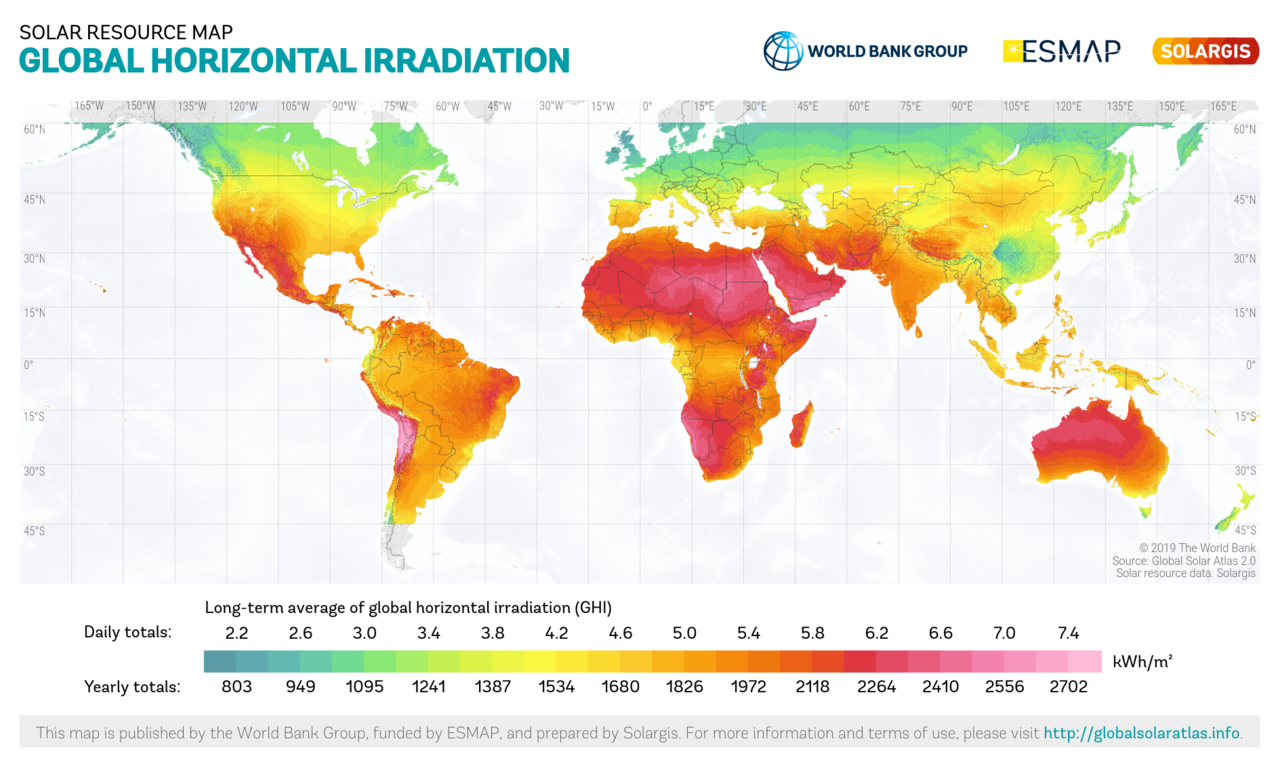 Fig.: Map of global irradiation on a horizontal plane.
Fig.: Map of global irradiation on a horizontal plane.
Please consider the different color scales! The two irradiance diagrams are not directly comparable!
Source: https://en.wikipedia.org/wiki/Solar_irradiance
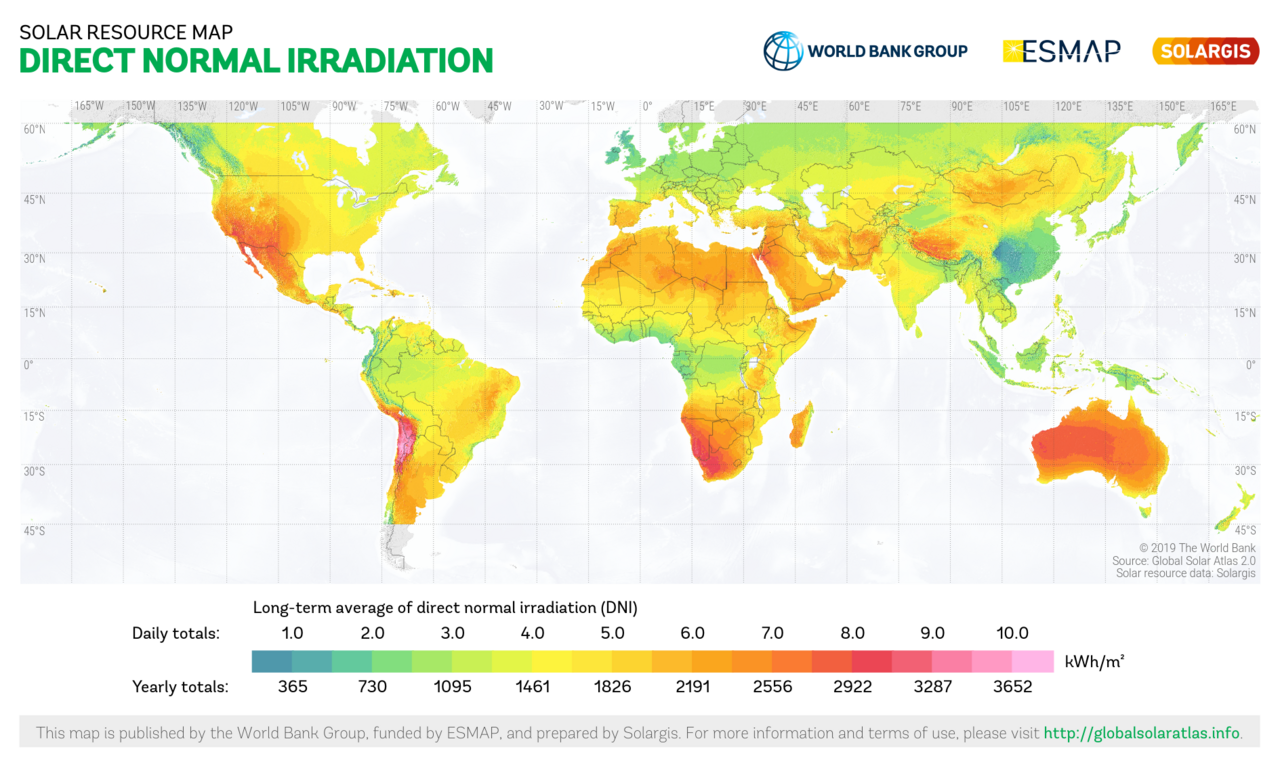
Fig.: Map of direct normal irradiation.
Please consider the different color scales! The two irradiance diagrams are not directly comparable!
Source: https://en.wikipedia.org/wiki/Solar_irradiance
Stirling Engine
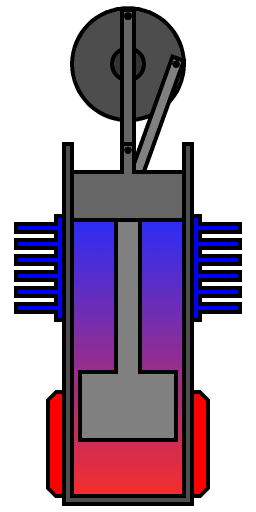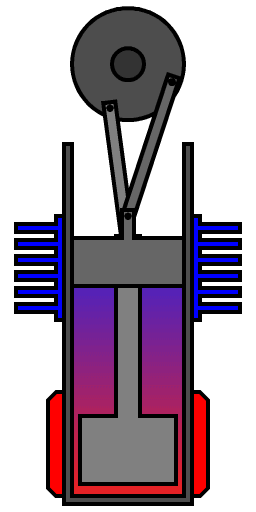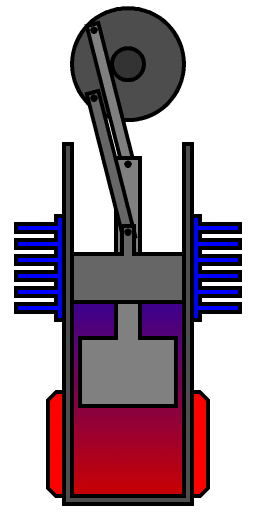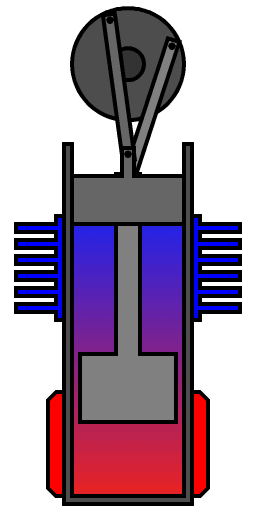
Fig.: Beta-type Stirling engine, with only one cylinder, hot at one end and cold at the other. A loose-fitting displacer shunts the air between the hot and cold ends of the cylinder. A power piston at the open end of the cylinder drives the flywheel.
Source: https://en.wikipedia.org/wiki/Stirling_engine/
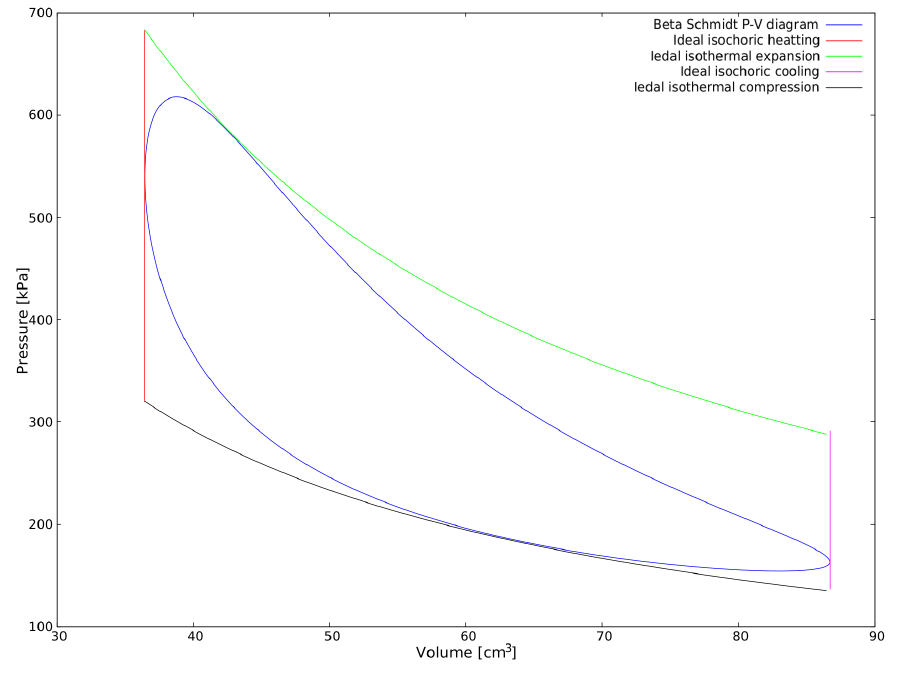
Fig.: P-V-diagram of a beta Stirling maschine: Ideal cycle vs. real cycle. The temperatures of the ideal isothermals are 400K and 850K , respectively.
Source: Egas, J. and Clucas D.M (2018)
Tasks / Questions
- What is concentrated solar power? What are advantages and disadvantages compared to photovoltaics?
- Is there any significant large scale CSP plant implementation?
- Assume you were an investor. Where in Europe would you try to install a large scale SCP plant? Explain.
- What do “direct normal irradiation” and “global horizontal irradiation” in the above diagrams mean?
- Assume the Dish-Stirling-System were equipped with a solar tracker collecting the direct normal component. What is the approximate irradiation energy per year in Almería (Spain) per 1 m² of solar collector? Read it from the diagrams above.
- Describe the working principle of a Stirling engine.
- Analyse the Stirling engine the P-V-diagram of which is shown above. Start with the ideal cycle. Take one of the corner points of the isothermals (400K and 850K). Assume air to be the working gas (diatomic). How many moles of air are in the machine?
- What are the total heat capacities under constant volume and constant pressure?
- In the lectures on thermodynamic cycles we set up and filled a table containing thermodynamic states as well as state transitions (aka processes) for an Otto engine. Set up a similar table and fill it for the Stirling machine under investigation (P-V-diagram above). Read the values from the diagram (as good as you can). Temperatures are given.
- What is the net work $W_\mathrm{net}$ of the machine?
- What is the heat input $Q_\mathrm{in}$ from the hot reservoir and the energy loss $Q_\mathrm{out}$ to the cold reservoir?
- What is the efficiency of that machine?
- Write a program in Python to be able to re-calculate all calculations easily when changing parameters. The following parameters should be modifiable: Lower and upper volume, lower and upper temperature, number of moles of diatomic working gas.
- The efficiency of an ideal Carnot machine depends on the two temperatures $T_c$ and $T_h$. Draw the efficiency as a function of $T_h$ (from 400K to 850K). Of course, it is not linearly dependent on temperature. This means, if you double the temperature difference you are not doubling the efficiency.
- Assume simply average annual conditions. You do not have to take irradiance variations (day time, season, weather) into account. Assume you had a mirrored dish following the sun and assume that the collected power by the dish is completely redirected to the hot end (the hot reservoir $T_h$) of the Stirling engine. How large has the dish to be (on average) to able to provide $Q_\mathrm{in}$ (on average)?
Expected Project Output
- Well-structured scientific report of approx. 5-10 pages content(!) (excluding title page, TOC, references, etc.)
- Program (Python)
- Video Tutorial
Material
The non-comprehensive list is for inspiration.
- Solar-Stirling-System: https://de.wikipedia.org/wiki/Solar-Stirling (only in German, use Google translate)
- Solar irradiance: https://en.wikipedia.org/wiki/Solar_irradiance
- Plataforma Solar de Almería: https://en.wikipedia.org/wiki/Plataforma_Solar_de_Almer%C3%ADa
- Parabolic trough: https://en.wikipedia.org/wiki/Parabolic_trough
- Ideal Stirling cycle (isothermal): https://en.wikipedia.org/wiki/Stirling_cycle
- More realistic Pseudo Stirling cycle (adiabatic): https://en.wikipedia.org/wiki/Pseudo_Stirling_cycle
- Stirling Engine: https://en.wikipedia.org/wiki/Stirling_engine
- Egas, J.; Clucas, D.M. Stirling Engine Configuration Selection. Energies 2018, 11, 584.
Online: https://www.mdpi.com/1996-1073/11/3/584 - Torres García, M.; Carvajal Trujillo, E.; Vélez Godiño, J.A.; Sánchez Martínez, D. Thermodynamic Model for Performance Analysis of a Stirling Engine Prototype. Energies 2018, 11, 2655.
Online: https://www.mdpi.com/1996-1073/11/10/2655
